02/28/2019

I recently decided to update my renderer (moving it to DX12 from DX11 and expanding it considerably). This is still a work in progress. As part of this revamping, I also decided to ditch Doxygen for building documentation and use Natural Docs (http://naturaldocs.org) instead. This tool makes some awesome looking documentation. Below is a link to some of the files I've already started to convert:

https://pat-sweeney.github.io/Caustic/

11/05/2018

So I've spent the last week learning PyTorch and Python. PyTorch is pretty awesome so far. Python on the other hand is such a crappy language. I don't understand why the ML world is so enamored with it. Yeah, its easy and for the most part concise; but it has some truly terrible features. I keep getting burned by its dumb scoping rules. Also, who in their right mind thinks indentation is a good scoping mechanism?!?. But the worst part is running some code that takes a while only to have it crash because it finally executes something that has syntax errors. Blech!

01/16/2019

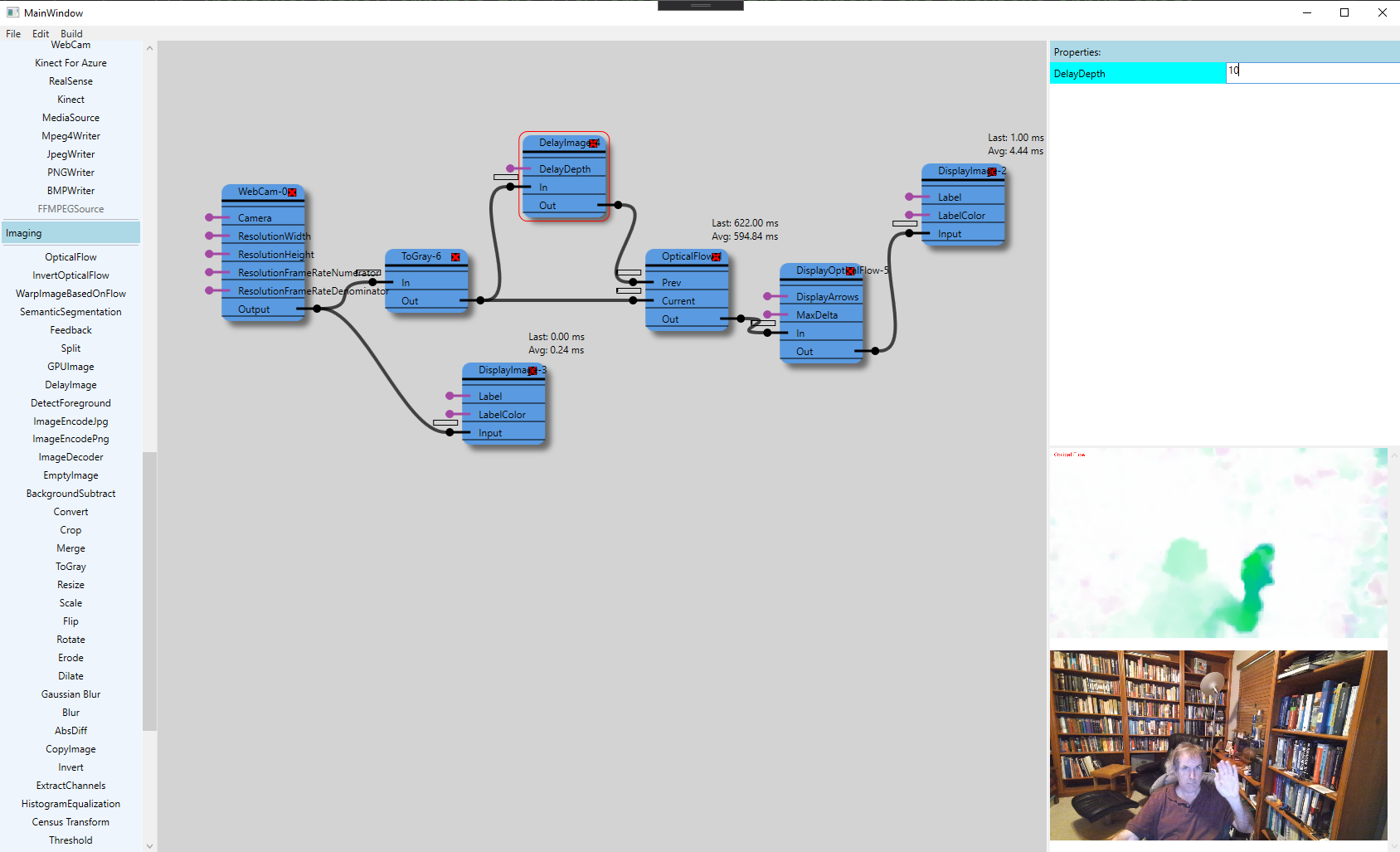
Had to rewrite some \Psi code for transforming an existing store. As a side tangent I decided to create a graphical tool for creating \Psi pipelines. WPF Rocks! Only took me a couple days to get a basic infrastructure up and running (supporting creating nodes, creating links, dragging around nodes, and generating backing code to match the created graph). Would have been a lot harder without WPF.

Update: Since writing this article I have added a lot more support to my tool, including support for more components, grouping, linkable parameters, tooltips, etc. I've also updated the screenshot.

10/09/2018

I recently had to solve a bug in my code that handles lens distortion. Below is the math that works out the inverse to the distortion model we use (Brown-Conrady model). I am putting this here for future reference. This model handles both radial distortion (by parameters $K_0$ and $K_1$) and tangential distortion (by parameters $T_0$ and $T_1$): $$ X_u = X_d (1 + K_0 r^2 + K_1r^4) + T_1(r^2+2X_d^2) + 2 T_0 X_d Y_d$$ $$ Y_u = Y_d (1 + K_0 r^2 + K_1r^4) + T_0(r^2+2Y_d^2) + 2 T_1 X_d Y_d$$ The formulas above compute a undistorted pixel coordinate ($X_u$,$Y_u$) from an distorted coordinate ($X_d$,$Y_d$). For going the other way (given an undistorted coordinate => distorted coordinate) we use Newton-Raphson to solve for $X_d$, $Y_d$ The math for doing this, although looking rather hairy, is rather straight forward. We want to solve the following equation for $X_d,Y_d$: $$ F(X_d,Y_d):= 0 = undistort([X_d,Y_d]) - [X_u,Y_u] $$ $$ F(X_d) := 0 = X_d (1 + K_0 r^2 + K_1r^4) + T_1(r^2+2X_d^2)+2 T_0 X_d Y_d - X_u$$ $$ F(Y_d) := 0 = Y_d (1 + K_0 r^2 + K_1r^4) + T_0(r^2+2Y_d^2)+2 T_1 X_d Y_d - Y_u$$ At each step of the optimization we want to update: $X_d$,$Y_d$ via: $$ X_d=X_{d-1} - J(F(X_d))^- * F(X_d)$$ $$ Y_d=Y_{d-1} - J(F(Y_d))^- * F(Y_d)$$ Where $J(F(X_d,Y_d))^-$ is the defined as the inverse of the Jacobian: $$ \begin{bmatrix}\frac{\partial F_{X_d}}{\partial X_d} & \frac{\partial F_{X_d}}{\partial Y_d} \\ \frac{\partial F_{Y_d}}{\partial X_d} & \frac{\partial F_{Y_d}}{\partial Y_d}\end{bmatrix}$$ Where: $r^2=X_d^2 + Y_d^2$
$\frac{\partial {r^2}}{\partial X_d} = 2 X_d$
$\frac{\partial {r^2}}{\partial Y_d} = 2 Y_d$
$\frac{\partial {r^4}}{\partial X_d}= 2r^2 2 X_d = 4 X_d r^2$
$\frac{\partial F_{X_d}}{\partial X_d} = (1 + K_0 r^2 + K_1 r^4) + X_d (K_0 \frac{\partial}{\partial X_d} r^2 + K_1 \frac{\partial}{\partial X_d} r^4) + T_1 \frac{\partial}{\partial X_d} r^2 + 4 T_1 X_d + 2 T_0 Y_d$
        $= (1 + K_0 r^2 + K_1 r^4) + X_d (K_0 2 X_d + K_1 4 X_d r^2) + T_1 2 X_d + 4 T_1 X_d + 2 T_0 Y_d$
$\frac{\partial F_{X_d}}{\partial Y_d} = X_d ( K_0 \frac{\partial}{\partial Y_d} r^2 + K_1 \frac{\partial}{\partial Y_d} r^4) + \frac{\partial}{\partial Y_d} T_1 r^2 + 2 T_0 X_d$
        $= X_d ( K_0 2 Y_d + K_1 4 Y_d r^2) + T_1 2 Y_d + 2 T_0 X_d$
$\frac{\partial F_{Y_d}}{\partial X_d} = Y_d ( K_0 \frac{\partial}{\partial X_d} r^2 + K_1 \frac{\partial}{\partial X_d} r^4) + \frac{\partial}{\partial X_d} T_0 r^2 + 2 T_1 Y_d$
        $= Y_d ( K_0 2 X_d + K_1 4 X_d r^2) + T_0 2 X_d + 2 T_1 Y_d$
$\frac{\partial F_{Y_d}}{\partial Y_d} = (1 + K_0 r^2 + K_1 r^4) + Y_d (K_0 \frac{\partial}{\partial Y_d} r^2 + K_1 \frac{\partial}{\partial Y_d} r^4) + T_0 \frac{\partial}{\partial Y_d} r^2 + 4 T_0 Y_d + 2 T_1 X_d$
        $= (1 + K_0 r^2 + K_1 r^4) + Y_d (K_0 2 Y_d + K_1 4 Y_d r^2) + T_0 2 Y_d + 4 T_0 Y_d + 2 T_1 X_d$
Finally, solving for $J(F(X_d))^-$ gives: $$J(F(X_d))^- = \frac{1}{\frac{\partial F_{X_d}}{\partial X_d} \frac{\partial F_{Y_d}}{\partial Y_d} - \frac{\partial F_{X_d}}{\partial Y_d} \frac{\partial F_{Y_d}}{\partial X_d}} \begin{vmatrix}\frac{\partial F_{Y_d}}{\partial Y_d} & \frac{ - \partial F_{X_d}}{\partial Y_d} \\ \frac{ - \partial F_{Y_d}}{\partial X_d} & \frac{\partial F_{X_d}}{\partial X_d}\end{vmatrix}$$ However, once I implemented this, it kept giving me the wrong results. For instance, in the following pictures you can see the distorted image on the left, and the resulting undistorted picture on the right.

If you look closely the image has weird discontinuities in both the distorted and undistorted images. These should look like:

The bug I had basically boiled down to assuming that 0.0001 is zero, which wasn't nearly small enough (used when testing for convergence).